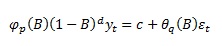The Johansen cointegration approach

The Johansen’s solution to cointegration is based on vector autoregression (VAR) and allows simultaneous analysis of n time series. With (n x 1) vector Xt the VAR model is defined (for simplicity neither intercept vector c, nor deterministic regressors CDt are considered):

This can be rewritten to a multivariate generalization of the Augmented Dickey-Fuller test:

This is the "transitory" form (because it includes Xt-1, as opposed to "long-run" form which includes Xt-p) therefore it holds that:

The rank r of the (n x n) matrix Π determines number of cointegration vectors (0≤r<n). If r=0 then there is no cointegration.  Matrix Π (impact matrix) can be rewritten to product of (n x r) matrix of adjustment parameters α and (r x n) matrix of cointegrating vectors β’.

For example, having two time series the VAR(1) and VECM(1) model become:

To find out r (number of cointegrating vectors), we can perform the “trace” test to test for:
H0: There are r (linearly-independent) cointegrating vectors (and n-r common stochastic trends)
H1: There are more than r cointegrating vectors
We usually start with r=0, perform the test and in case of rejection we increase r by 1 and test again, until the hypothesis is not rejected.


An example in R code (taken from Bernhard Pfaff: Tutorial - Analysis of Integrated and Cointegrated Time Series) :


set.seed(12345)
e1 <- rnorm(250, 0, 0.5)
e2 <- rnorm(250, 0, 0.5)
e3 <- rnorm(250, 0, 0.5)
u1.ar1 <- arima.sim(model = list(ar=0.75), innov = e1, n = 250)
u2.ar1 <- arima.sim(model = list(ar=0.3), innov = e2, n = 250)
y3 <- cumsum(e3)
y1 <- 0.8 * y3 + u1.ar1
y2 <- -0.3 * y3 + u2.ar1
ymax <- max(c(y1, y2, y3))
ymin <- min(c(y1, y2, y3))
plot(y1, ylab = "", xlab = "", ylim = c(ymin, ymax))
lines(y2, col = "red")
lines(y3, col = "blue")
y.mat <- data.frame(y1, y2, y3)
vecm1 <- ca.jo(y.mat, type = "eigen", spec = "transitory")
vecm2 <- ca.jo(y.mat, type = "trace", spec = "transitory")
vecm.r2 <- cajorls(vecm1, r = 2)
vecm.level <- vec2var(vecm1, r = 2)
vecm.pred <- predict(vecm.level,n.ahead = 10)
fanchart(vecm.pred)
vecm.irf <- irf(vecm.level, impulse = 'y3',response = 'y1', boot = FALSE)
vecm.fevd <- fevd(vecm.level)
vecm.norm <- normality.test(vecm.level)
vecm.arch <- arch.test(vecm.level)
vecm.serial <- serial.test(vecm.level)

The Engle-Granger cointegration approach

The two steps of Engle-Granger’s approach to cointegration, in case of two time series yt, xt, are:

1st step:
Test for integration order of both variables (as it is condition for cointegration that all variables are integrated of same order I(d)). This is achieved  (for instance) via the Augmented Dickey-Fuller test (any of the three variants can be used, according to judgment). If both variables are integrated of same order, least square regression cointegrating model can be estimated:

The residuals ût are then tested for stationarity (Augmented Dickey-Fuller test without drift and without trend,  however since residuals are themselves estimates, the MacKinnon critical values have to be used). If time series of residuals is found stationary, the two time series are said to be cointegrated .


2nd step:
Estimate error correction model with residuals ût (from step 1). As the estimate of β̂ is superconsistent, the residuals can be considered to be “known” and then ordinary least square applies:

An example in R code (taken from Bernhard Pfaff: Tutorial - Analysis of Integrated and Cointegrated Time Series) :




set.seed(12345)
e1 <- rnorm(250, mean = 0, sd = 0.5)
e2 <- rnorm(250, mean = 0, sd = 0.5)
u.ar3 <- arima.sim(model = list(ar = c(0.6, -0.2, 0.1)), n = 250, innov = e1)
y2 <- cumsum(e2)
y1 <- u.ar3 + 0.5*y2
ymax <- max(c(y1, y2))
ymin <- min(c(y1, y2))
layout(matrix(1:2, nrow = 2, ncol = 1))
plot(y1, xlab = "", ylab = "", ylim =c(ymin, ymax), main ="Cointegrated System")
lines(y2, col = "green")
plot(u.ar3, ylab = "", xlab = "", main = "Cointegrating Residuals")
abline(h = 0, col = "red")
lr <- lm(y1 ~ y2)
ect <- resid(lr)[1:249]
dy1 <- diff(y1)
dy2 <- diff(y2)
ecmdat <- cbind(dy1, dy2, ect)
ecm <- dynlm(dy1 ~ L(ect, 1) + L(dy1, 1)+ L(dy2, 1) , data = ecmdat)

Cointegration and error correction model

If two (or more) time series are integrated of same order (e.g. of order one I(1)), but their linear combination is integrated of lesser order (e.g. integrated of order zero I(0)), then these series are cointegrated.


In the vector notation: if yt is (n x 1) vector of time series (y1,t, y2,t, ... yn,t)' all integrated of order I(d) and β is (n x 1) cointegrating vector (β1, β2, ... βn)' , then if there exists linear combination zt integrated of order I(d-b), the vector of time series is cointegrated I(d,b).

In fact, there can be more than one cointegrating vectors, then we are dealing with (n x r) matrix β. There can be 0<r<n cointegrating vectors. It follows that there are n-r common stochastic trends.



One advantage of cointegration is that the problem of “spurious regression” can be avoided in this case, as the least square regression gives unbiased and superconsistent estimates.


Another advantage is that it is a long-term model (e.g. captures long-term relationship between levels of two time series y and x) in contrary to a model fitted on differenced data which would be a short-term model (e.g. captures effect of change in x on change of y). Combination of both approaches (short- and long-term models) is known as error correction model (ECM), which is self-regulating model that allows for short-term autoregressive behavior but after some time always aligns time series into equilibrium given by cointegrating vectors.


To test for cointegration and to create an error correction model, several approaches are possible, most common are the Engle-Granger's two step estimation and Johansen‘s vector autoregressive (VAR) technique. While the Engle-Granger's approach is easier to perform, it allows only one cointegrating vector at most (one has to decide which of the series is dependent and which are idependent).

The one sample t-test (coefficient significance test)

In the one sample t-test we are testing whether population mean parameter μ equals some value μ0:


H0: μ=μ0
H1: μ<>μ0


Given sample of independent measurements xi for i=1..n with sample mean x̅ and sample standard deviation s, the t statistics is defined as:

The t statistics follows Student’s t-distribution with n-1 degrees of freedom under the null hypothesis.


To test for significance of an estimated coefficient β̂ in a (regression or ARIMA) model with p predictors, we test whether mean value of coefficients is equal to 0 (β0=0) :

The degrees of freedom decrease with each parameter. For instance, for linear regression model:

Because there are p predictors and one intercept.




An example in R language:




a=c(1,2,3,4,2,3,6,7,8)
b=c(1,2,3,4,8,2,4,1,2)
c=c(1,2,6,4,2,3,0,1,9)
d=c(1,2,0,4,2,1,0,1,8)
m1=lm(a~b+c+d)
summary(m1)
coeff=summary(m1)$coefficients[,1]
stderr=summary(m1)$coefficients[,2]
pdf=pt(q=(coeff/stderr),df=(length(a)-length(coeff)))
ifelse(pdf>.5,1-pdf,pdf)*2

Time series (theoretical concept)

A time series is a collection of random variables {Y1,Y2,…YT} ordered in time. There is a stochastic process {Yt} that generates the series. Each element Y1,Y2,…YT of the series is a random draw from a probability distribution. However we can only observe one particular realization of the stochastic process {y1,y2,..yT} in reality.



The stochastic process {Yt} is then described by a T-dimensional joint probability distribution. The(unknown) parameters (mean, variance, covariance) of the joint probability distribution of {Yt} are, for each t=1,2…T:

For a weakly stationary time series it holds that:

To infer the parameters from a particular observed realization, we assume the process to be ergodic (the sample moments approach the population moments as T becomes infinite).

The constant in ARIMA model

The non-seasonal ARIMA model is defined as:

To rewrite it in the form including drift term:

It is implemented that way in R package forecast (Rob J. Hydman). The R implementation has one more catch – the moving average polynomial is defined with a "+" instead of "-":

When d=0, the μ is called “mean”.
When d=1, the μ is called “drift”.
Simple t-test can be used to test for μ parameter significance.
The c constant can be rewritten into μ form:

The μ is the mean of differenced time series (not same as “sample mean” due to autocorrelation).

The Dickey-Fuller unit root test (stationarity test)

The Dickey-Fuller test is a unit root test. Presence of unit root is only one of potential causes of non-stationarity, therefore in the strict sense it is not a comprehensive stationarity test.


The hypotheses are set in following way:
H0: unit root is present in the sample
H1: stationarity or trend-stationarity

Definition of unit root is based on characteristic equation. Having autoregressive process (with zero-mean, no autocorrelation and constant variance error εt):

Then m is root of characteristic equation:

If m=1 then it is a unit root.

In case of first order autoregressive process the characteristic equation becomes:

In this example, the m is unit root (m=1) if just when γ1=1.


If there is unit root in this first order autoregressive process, the process is non-stationary (it is integrated of order one I(1)) as its properties depend on particular time t:

Therefore to test unit root presence in first order autoregressive process AR(1):

Depending on what is the hypothesis, the testing regression model differs:
If hypothesis is a unit root process:

If hypothesis is a unit root process with drift:

If hypothesis is a unit root process with drift and time trend:

We are testing whether δ=0 (γ=δ+1=1), that is null hypothesis of unit root presence. However the testing statistic t does not have standard distribution. Instead Dickey-Fuller distribution tables have to be used (which are specific for each of three stated null hypothesis).


Apparently the test has low power (ability to reject the null if alternative is true) because it’s difficult to distinguish unit root from root near but less than one. It is therefore encouraged to really follow “graphics” and “common sense” before performing actual hypothesis test (Bo Sjo: Testing for Unit Roots and Cointegration).


To decide which of the tree variants of test shall be used, it’s best to rely on the knowledge about the nature of time series (is the presence of intercept or slope a rational expectation given the time series?). If such knowledge is missing, other approaches can be considered (Dolado, Jenkinson, Sosvilla-Rivero: Cointegration and Unit Roots).


Since the null hypothesis is non-stationarity (while in some other tests the null is stationarity, e.g. KPSS test), it is good idea to apply Dickey-Fuller test anytime we have good reason to believe the series is non-stationary (Bo Sjo: Testing for Unit Roots and Cointegration).
We are testing whether time series is I(1) - integrated of order one. If the time series is already differenced we are testing I(2). In such case if the I(2) is not rejected then it makes no sense to test for I(1) anymore.


The Augmented Dickey-Fuller test is a natural extension of the simple test by adding p lags to the process, hereby considering autoregression beyond first order:

Setting order p is an interesting question though. It is suggested to start with higher lags and cut it down continually. Alternatively information criteria (AIC, BIC, …) can be used.


The R adf.test function that is often used tests the third form of hypothesis (incl. intercept and slope). The R ur.df or adfTest  functions enables choosing of appropriate null hypothesis.