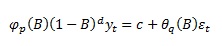The constant in ARIMA model

The non-seasonal ARIMA model is defined as:

To rewrite it in the form including drift term:

It is implemented that way in R package forecast (Rob J. Hydman). The R implementation has one more catch – the moving average polynomial is defined with a "+" instead of "-":

When d=0, the μ is called “mean”.
When d=1, the μ is called “drift”.
Simple t-test can be used to test for μ parameter significance.
The c constant can be rewritten into μ form:

The μ is the mean of differenced time series (not same as “sample mean” due to autocorrelation).

The Dickey-Fuller unit root test (stationarity test)

The Dickey-Fuller test is a unit root test. Presence of unit root is only one of potential causes of non-stationarity, therefore in the strict sense it is not a comprehensive stationarity test.


The hypotheses are set in following way:
H0: unit root is present in the sample
H1: stationarity or trend-stationarity

Definition of unit root is based on characteristic equation. Having autoregressive process (with zero-mean, no autocorrelation and constant variance error εt):

Then m is root of characteristic equation:

If m=1 then it is a unit root.

In case of first order autoregressive process the characteristic equation becomes:

In this example, the m is unit root (m=1) if just when γ1=1.


If there is unit root in this first order autoregressive process, the process is non-stationary (it is integrated of order one I(1)) as its properties depend on particular time t:

Therefore to test unit root presence in first order autoregressive process AR(1):

Depending on what is the hypothesis, the testing regression model differs:
If hypothesis is a unit root process:

If hypothesis is a unit root process with drift:

If hypothesis is a unit root process with drift and time trend:

We are testing whether δ=0 (γ=δ+1=1), that is null hypothesis of unit root presence. However the testing statistic t does not have standard distribution. Instead Dickey-Fuller distribution tables have to be used (which are specific for each of three stated null hypothesis).


Apparently the test has low power (ability to reject the null if alternative is true) because it’s difficult to distinguish unit root from root near but less than one. It is therefore encouraged to really follow “graphics” and “common sense” before performing actual hypothesis test (Bo Sjo: Testing for Unit Roots and Cointegration).


To decide which of the tree variants of test shall be used, it’s best to rely on the knowledge about the nature of time series (is the presence of intercept or slope a rational expectation given the time series?). If such knowledge is missing, other approaches can be considered (Dolado, Jenkinson, Sosvilla-Rivero: Cointegration and Unit Roots).


Since the null hypothesis is non-stationarity (while in some other tests the null is stationarity, e.g. KPSS test), it is good idea to apply Dickey-Fuller test anytime we have good reason to believe the series is non-stationary (Bo Sjo: Testing for Unit Roots and Cointegration).
We are testing whether time series is I(1) - integrated of order one. If the time series is already differenced we are testing I(2). In such case if the I(2) is not rejected then it makes no sense to test for I(1) anymore.


The Augmented Dickey-Fuller test is a natural extension of the simple test by adding p lags to the process, hereby considering autoregression beyond first order:

Setting order p is an interesting question though. It is suggested to start with higher lags and cut it down continually. Alternatively information criteria (AIC, BIC, …) can be used.


The R adf.test function that is often used tests the third form of hypothesis (incl. intercept and slope). The R ur.df or adfTest  functions enables choosing of appropriate null hypothesis.

Stationarity in time series

Formally: A time series y1,y2,... is nonstationary if, for some m, the joint probability distribution of yi, yi+1, ..., yi+m-1 is dependent on the time index i (definition by WolframMathworld)


Strong form of stationarity: A time series whose joint probability distribution does not change in time


Weak form of stationarity: A time series whose mean and autocovariance do not change in time (i.e. mean is the same at any time and covariance only depends on lag, not on time).


Practically: If the time series appear mean-reverting it is most probably stationary. If, on the contrary, it is drifting up or down, it is probably not. If the autocorrelation function drops to zero quickly on higher lags, it is probably stationary. On the contrary, ACF for non-stationary time series decreases very slowly. "Time series with trends, or with seasonality, are not stationary. A time series with cyclic behavior is stationary - that is because the cycles are not of fixed length, so before we observe the series we cannot be sure where the peaks and troughs of the cycles will be" (Rob J. Hydman: Forecasting: principles and practice).


The problem with non-stationarity is also known as “spurious regression” problem. When dealing with two (or more) non-stationary time series, very high correlation is often found between them, despite lack of any rational causality. What is often overlooked and ignored in many studies is that the correlation and regression coefficients might be misleading if assumptions (non-stationarity) are not met. The problem is that sample estimates of correlation and regression coefficients can not be interpreted as population parameters at all in such case (Johansen: Correlation, regression, and cointegration of nonstationary economic time series).


Treatment of non-stationarity is possible:

• If there is a deterministic trend, the time series can be in fact “trend stationary process” as it mean-reverts to a level determined for each time t by function f(t) (e.g. linear time trend f(t)=βt). By simply subtracting trend f(t) we obtain stationary process.
• If the series drifts up or down (the process is not mean-reverting because stochastic shocks persists a.k.a. there is a unit root) then differencing helps. Typical example would be random walk process.
• If there is deterministic seasonality, set of dummy variables can capture the seasonal component.
• If there is changing seasonal effect, then seasonal differencing helps.
• If there is increasing variance, log transformation can be applied (to remedy the variance problem in general, the Box-Cox transformation function helps).

The ultimate goal of non-stationarity remedies should be however to obtain stationary residuals. A model with non-stationary dependent or independent variables should not present a problem as long as model errors are stationary. A prime example would be cointegration model, which is a correct model describing two processes which evolve in an equilibristic relationship.

ARIMA examples

To better understand specifics of different ARIMA models (incl. some interesting prototypes), I fitted the models on sample time series. I chose a temperature time series measured hourly, where it is reasonable to assume both - cycle and drift (in this sense the temperature series is not much different from daily measured series of current account balances).


The predicted mean and 99% interval is illustrated. Models with zero differencing have constant for level, models with one differencing (ordinary or seasonal) have constant for drift and models with two differencings (ordinary or seasonal or mixed) do not have constant as the trend is modeled as random here.

It was generated in R:

library("zoo")

library("forecast")

d<-read.csv(file="Temperature.csv",sep=";")

y<-ts(d$Temperature,frequency = 24)


cut=13 # division between in and out sample

h=8 # forecast horizon

fitModel<-function(p,d,q,P,D,Q,title)

{
insample=window(y,start=c(1,1),end=c(cut,frequency(y)))
outsample=window(y,start=c(cut+1,1),end=c(cut+h,frequency(y)))

# in sample fit

fitIn <- Arima(insample,order=c(p,d,q),seasonal=c(P,D,Q),include.constant = T)
print(fitIn)
plot(forecast(fitIn,h=h*frequency(y)),main=paste(title,": (",paste(p,d,q,P,D,Q,sep=","),")"),ylim=c(-20,20),cex.main=.9)
lines(outsample,col="red",lt=1)+abline(h=c(-10,0,10),col="darkgreen",lt=2)
#lines(fitted(fitIn),col="green",lw=1)

# out of sample accuracy

#fitOut <- Arima(outsample,model=fitIn)
#accuracy(fitIn) # out-of-sample one-step forecasts.
#accuracy(fitOut) # out-of-sample multi-step forecasts
#print(fitIn)
#print(fitOut)
}

par (mfrow=c(2,2))

fitModel(0,0,0,0,0,0,"white noise")
fitModel(0,1,0,0,0,0,"random walk")
fitModel(1,1,0,0,0,0,"differenced autoregressive")
fitModel(5,1,0,0,0,0,"differenced autoregressive")

fitModel(0,1,1,0,0,0,"differenced moving average (exponential smoothing)")

fitModel(0,1,5,0,0,0,"differenced moving average")
fitModel(0,2,2,0,0,0,"linear exponential smoothing")
fitModel(1,1,2,0,0,0,"damped linear exponential smoothing")

fitModel(0,0,0,1,1,0,"seasonal differenced autoregressive")

fitModel(1,0,0,1,1,0,"seasonal differenced autoregressive")
fitModel(0,0,0,0,1,1,"seasonal differenced moving average")
fitModel(0,0,1,0,1,1,"seasonal differenced moving average")

fitModel(1,1,0,0,1,0,"seasonal random trend autoregressive")

fitModel(1,1,0,1,1,0,"seasonal random trend autoregressive")
fitModel(0,1,1,0,1,0,"seasonal random trend moving average")
fitModel(0,1,1,0,1,1,"seasonal random trend moving average")
par (mfrow=c(1,1))

ARIMA prototypes

There are some interesting prototypic ARIMA models. In fact the ARIMA framework is that much general that it covers whole list of time series models:


ARIMA(0,0,0) is white noise (with optional level based on c):

ARIMA(0,1,0) is random walk (with opt. drift based on c):

ARIMA(1,1,0) is differenced first-order autoregressive model (with opt. drift based on c):

ARIMA(0,1,1) is exponential smoothing (with opt. drift based on c):

ARIMA(0,2,2) is linear exponential smoothing (with opt. curvature based on c):

ARIMA(1,1,2) is damped-trend linear exponential smoothing (with opt. drift based on c):

ARIMA(0,0,0)(1,1,0)12 is annually differenced first-order autoregressive model (with opt. drift based on c):

ARIMA(0,1,0)(0,1,0)12 is annual random trend model (with opt. curvature based on c):

It is also interesting to show that AR and MA terms can mimic differencing (more on this in Robert Nau: Statistical forecasting: notes on regression and time series analysis). It's easiest to explain on ARIMA(1,1,1) model:

It is evident, that if ϕ→1 it mimics the differencing (1-B) and, on the contrary, if θ→1 it mimics integrating, as the (1-B) on both sides of equation “cancel each” other. In a similar way if ϕ≈θ the (1- ϕB) “cancels” (1- θB) out.



It is also shown that a MA model can be expressed as infinite AR model (and vice versa). Consider simple MA(1):

Then with the “hack” of infinite geometric series expression:

Possible lesson from the “mimicking” topic would be: do not “overfit” by trying model where simultaneously both (AR and MA) term orders are 2 or more (e.g. ARIMA(2,1,2)) because the terns might cancel each other out.